Intact Stability

This page outlines the main terms and elementary principles related to intact stability.

Intact stability

What is stability?

Stability is the ability of a vessel to float in an upright position, and if inclined by an external heeling force, it returns to the upright position when the external force is removed.

Stability does not refer to a particular direction, whether longitudinally or transversely. However, as the ship will predominantly experience transverse inclinations, it is transverse stability that is most important to the ship’s master.

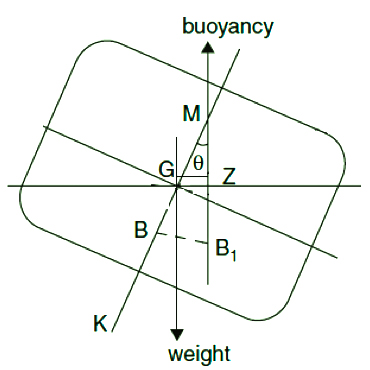
Transverse stability can be defined regarding the initial metacentre (M), metacentric-height (GM) and the righting arm (GZ).

***

What external forces can cause a ship to heel?

A ship can experience a heeling moment due to:

  1. windage;
  2. turning forces when altering course; and
  3. waves and swelled action.

***

Explain the term Archimedes Principle?

Archimedes principle is a law of fluid dynamics which states that vessels that are submerged or possibly submerged in a liquid experience a force of buoyancy:

  • equal to the weight of water displaced;
  • acting in an upward direction;
  • from the centre of the mass of the displaced fluid

From this, we can see that the forces of buoyancy pressing against the hull can be resolved into a single point (B) and that a line of force acts upwards from this point.

What is the initial metacentre (M)?

When a ship is floating at rest in still water, the force of buoyancy (B) acts upwards in a vertical line from a single point which is resolved at the transverse centre of the displaced water volume.

When the same ship is then inclined by an external force and heels to a small angle, a buoyancy wedge will cause B to shift to the low side. This force will continue to act upwards in a new straight line, or vector, from a new position B1.

The two lines of force acting upwards from B and B1 converge at a well-defined point, and will consistently do so for all small angles of the heel.

This point of intersection of the lines of force and vectors of B for angles of heel up to 10 degrees, is called the metacentre (M).

We can therefore think of the metacentre as the virtual point from which the vessel is suspended.

How is the position of M on the ship defined?

The position of M, for small angles of heel, is stated as a relative distance to the baseline, or keel plate, and is referred to as KM, where KM = KB + BM.

The KM value changes with the draught of the ship and is given in the metacentric diagram or tables contained within the ship stability information.

***

What is the metacentric height (GM)?

The weight of the ship, and all its fixed and moveable masses, act individually downward in vertical lines towards the centre of the earth. Each of these individual weights however can, for practical purposes, be resolved into a single point called the centre of gravity (G).

The metacentric height is the relative distance, measured in metres, between the positions of the vertical centre of gravity (G) and the metacentre (M).

It is referred to as GM and provides a measure of the vessel’s stability.

We consider M the point from which the ship G is virtually suspended, so we can think of GM as a kind of pendulum always seeking to return to rest.

***

 

How does GM indicate the state of a vessel’s stability?

The relative positions of G and M are important regarding their effect on the stability of a floating vessel at small angles of the heel.

Where G is above M, then the vessel has negative stability and will suffer a loll.

Where G and M are in the same position, then the vessel has neutral stability.

In a ship where G is physically below M, then the vessel has positive stability.

***

What is the righting arm?

As described, when a ship with positive stability is floating in an upright condition, G acts vertically downwards and B acts vertically upwards. When the two opposing forces act in the same line, the vessel is in equilibrium.

When the same vessel is heeled to a small angle by an external heeling force, the position of B moves out towards the submerged side to a new position B1. Because of this, the two opposing forces of downward G and upward B1 are no longer acting in line with each other.

This distance between the line of force of upward-acting B1 from the line of force of downward-acting G creates a turning moment (or lever) acting to return the vessel to the upright position.

The point of closest distance from the line of force acting up from B1 from the downward-acting G is called Z.

The distance of GZ is known as the righting lever or righting arm.

***

What are stiff and tender conditions?

When a vessel’s righting lever is too large, the vessel will quickly return to the upright when heeled. This is called a stiff and can be observed by violent movements of the ship when returning to the upright. The roll period of the ship will be short.

When a GZ is too small, the vessel will return slowly to the upright when heeled. This is called a tender condition and can be observed particularly when the vessel seems to hang in a listed position before eventually returning to the upright. The roll period of the ship will be long.

***

What is a free surface effect?

Free surface effect is a virtual loss of GM caused by the change of the centre of gravity for liquid tanks that are not completely filled.

Loss of GM (m) =

(Free surface moment ™ x specific gravity of the liquid) / vessel displacement

***   ***   ***   ***   ***

Thanks for reading this far. Have I covered everything? Is there anything that I have missed? Please comment below.

New content will regularly be added to TheMasterMariner.com, so please subscribe for the latest updates.